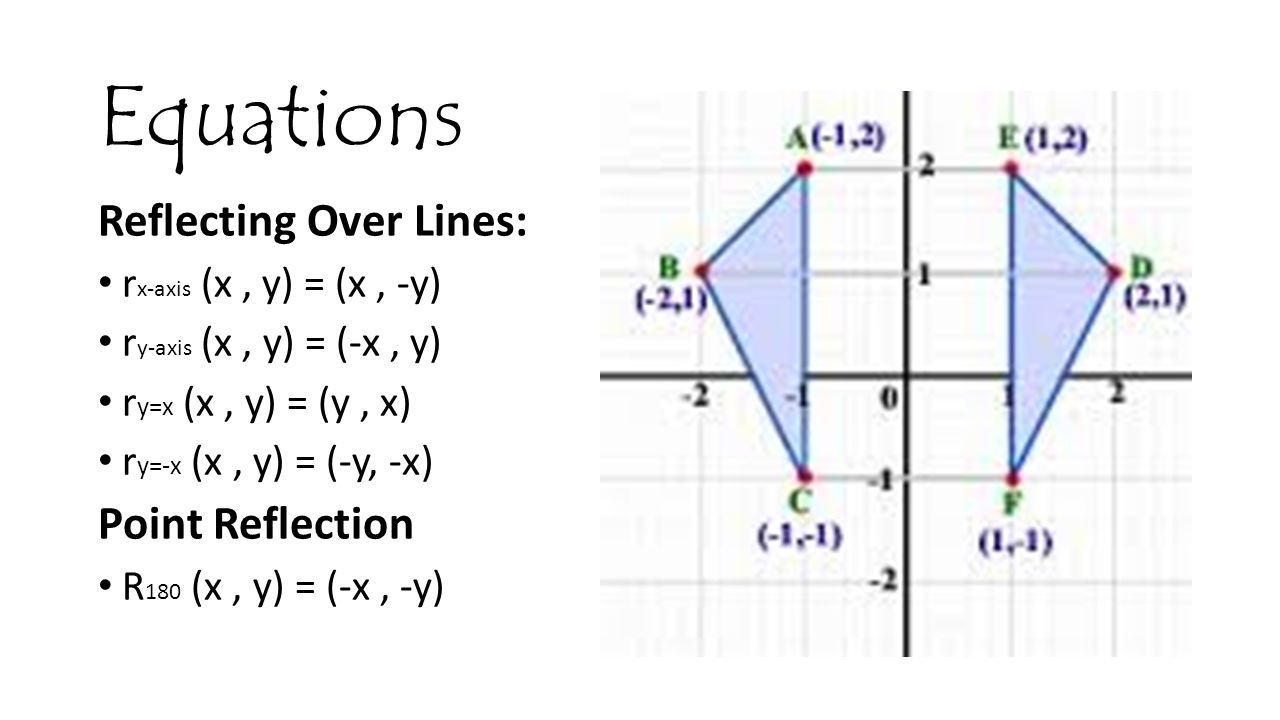
[ベスト] r y=x transformation 338403-After the transformation r y x the image of triangle abc

If you take any point x and repeatedly apply this transformation, the orbit that is produced is a spiral toward the origin Logarithmic spirals whose equations in polar coordinates r= c2 2 =ˇare invariant subsets of this rotary contraction, where cis any constant Transformations of R3 A 3 3 matrix describes a transformation of space, that is, aFind the image of A(4, 2) under the transformation ry=x?When a transformation maps vectors from \(R^n\) to \(R^m\) for some n and m (like the one above, for instance), then we have other methods that we can apply to show that it is linear For example, we can show that T is a matrix transformation, since every matrix transformation is a linear transformation

Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines

After the transformation r y x the image of triangle abc

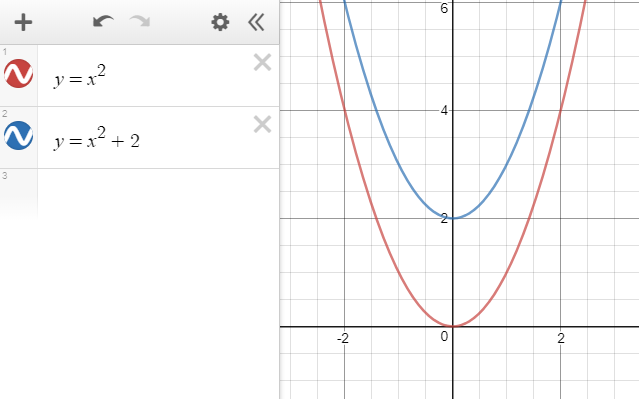
After the transformation r y x the image of triangle abc-Get your answers by asking now Ask Question 100 Join Yahoo Answers and getFor a better explanation, assume that y = x2 y = x 2 is f (x) = x2 f ( x) = x 2 and y = x2 y = x 2 is g(x) = x2 g ( x) = x 2 f (x) = x2 f ( x) = x 2 g(x) = x2 g ( x) = x 2 The transformation being described is from f (x) = x2 f ( x) = x 2 to g(x) = x2 g ( x) = x 2 f (x) = x2 → g(x) = x2 f ( x) = x 2 → g ( x) = x 2

Helmert Transformation Wikipedia

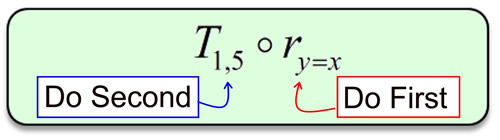
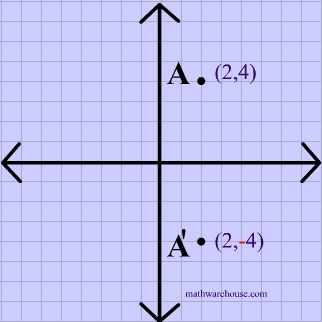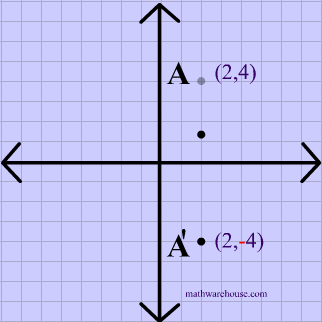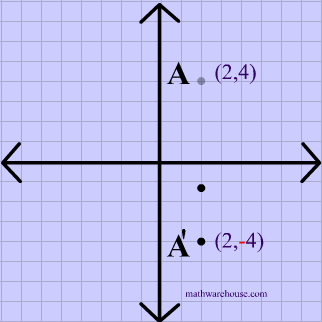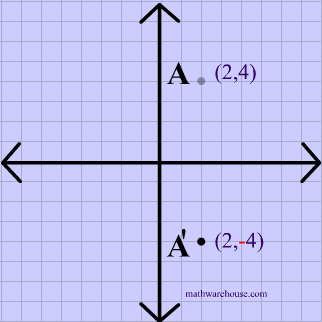
Called a linear transformation from R2 to R3 Definition 31 Let Vand Wbe two vector spaces Let Lbe a function defined on V with values in W Lwill be called a linear transformation if it satisfies the following two conditions 1 L(xy) = L(x)L(y), for any two vectors xand yin V 109(2, 4) (2, 4) (4, 2) (4, 2) Answer Save 2 Answers Relevance mohamharbi 1 decade ago Favorite Answer the answer is (2,4) r u fowler student??The symbol for a composition of transformations (or functions) is an open circle A notation such as is read as "a translation of (x, y) → (x 1, y 5) after a reflection in the line y = x" You may also see the notation written as This process must be done from right to left Composition of transformations is not commutative

What are the coordinates of point A' , the image of point A(4, 1) after the composite transformation R 90 o r y=x where the origin is the center of rotation?CT (x) = T (cx) Where T is your transformation (in this case, the scaling matrix), x and y are two abstract column vectors, and c is a constant If these two rules work, then you have a linear transformation ) Comment on eamanshire's post "Usually you should just use these two rules T (x)"To prove that T is a linear transformation, note that for any x, y ∈ R 2, if we write x = x 1 x 2, y = y 1 y 2, then we have T ( x y) = T ( x 1 y 1 x 2 y 2) = 2 ( x 1 y 1) ( x 2 y 2) 0 = 2 x 1 x 2 0 2 y 1 y 2 0 = T ( x) T ( y) Next, for any scalar r, we have T ( r x) = T ( r x 1 x 2) = T ( r x 1 r x 2) = 2 r x 1 r x 2 0 = r 2 x 1 x 2 0 = r T ( x)

23 The letter R is graphed at the origin Write compositions of transformations that would take the original R into each of the three transformed Rs labeled a, b and c Note There is more than one right answer for each of these Keep it simple b y x a cReflection over line y = x T(x, y) = (y, x) Rotations Turning Around a Circle A rotation is a transformation that is performed by "spinning" the object around a fixed point known as the center of rotationSee the answer answer both questions please Show transcribed image text Expert Answer

Www Sfponline Org Uploads 387 Geoch8reviewsolutions Pdf

Www Pmschools Org Site Handlers Filedownload Ashx Moduleinstanceid 701 Dataid 3614 Filename 15 composition of transformations answers Pdf

A reflection is a transformation representing a flip of a figure Figures may be reflected in a point, a line, or a plane When reflecting a figure in a line or in a point, the image is congruent to the preimage A reflection maps every point of a figure to an image across a fixed line A reflection of a point over the line y = − x is shownRecall from this definition in Section 31 that the identity transformation is the transformation Id R n R n → R n defined by Id R n (x)= x for every vector x Example (The standard matrix of the identity transformation)A geometry translation is an isometric transformation, meaning that the original figure and the image are congruent Translating a figure can be thought of as "sliding" the original If the image moved left and down, the rule will be (x __, y __) where the blanks are the distances moved along each axis;

Transformation Of Function Of A Random Variable Univariate Transformations Probability Density Function Statistical Theory

Desmos 2 Transformations Of Graphs Cambridge Maths Hub

0 0 Anonymous 1 decade ago?Transformation Rules (x,y)> STUDY Flashcards Learn Write Spell Test PLAY Match Gravity Created by caseymbarlow1 Terms in this set (11) Left h (xh, y) Right h (xh, y) Up k (x, yk) Down k (x, yk) Reflect xaxis (x, y) Reflect yaxis (x, y) Reflect y=x (y, x) Reflect y=x (y,x) 90 degrees CCW (y, x) 180 degrees CCW (x,y) 270F(x,y) = input image on which transformation function has to be applied G(x,y) = the output image or processed image T is the transformation function This relation between input image and the processed output image can also be represented as s = T (r) where r is actually the pixel value or gray level intensity of f(x,y) at any point

Www Pmschools Org Site Handlers Filedownload Ashx Moduleinstanceid 701 Dataid 3614 Filename 15 composition of transformations answers Pdf

Www Twinsburg K12 Oh Us Downloads Chapter 9 review 18 answer key 3 Pdf

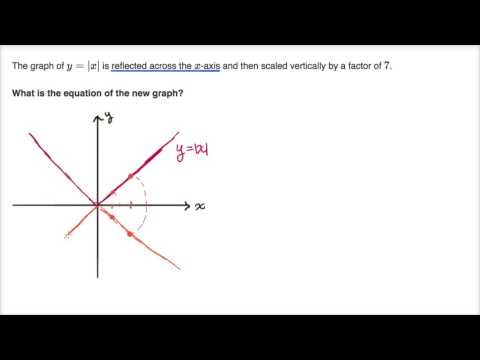
Check all that applyCombining Vertical and Horizontal Shifts Now that we have two transformations, we can combine them Vertical shifts are outside changes that affect the output (y) values and shift the function up or downHorizontal shifts are inside changes that affect the input (x) values and shift the function left or rightCombining the two types of shifts will cause the graph of a function to shift upFor translations left and up (x

2

Cardozohigh Com Ourpages Auto 16 12 23 Aim 16e cl composition take home quiz Pdf

In technical speak, pefrom the following transformation r(y=x)?Transformations of Random Variables September, 09 We begin with a random variable Xand we want to start looking at the random variable Y = g(X) = g X where the function g R !R The inverse image of a set A, g 1(A) = fx2R;g(x) 2Ag In other words, x2g 1(A) if and only if g(x) 2A For example, if g(x) = x3, then g 1(1;8) = 1;2A geometry translation is an isometric transformation, meaning that the original figure and the image are congruent Translating a figure can be thought of as "sliding" the original If the image moved left and down, the rule will be (x __, y __) where the blanks are the distances moved along each axis;

2

Schoolwires Henry K12 Ga Us Cms Lib08 Ga Centricity Domain 26 7th and 8th grade math 8th grade flexbook Unit 1 sections 1 23 1 4 rules for reflections Pdf

613 Projections along a vector in Rn Projections in Rn is a good class of examples of linear transformations We define projection along a vector Recall the definition 526 of orthogonal projection, in the context of Euclidean spaces Rn Definition 614 Suppose v ∈ Rn is a vector Then, for u ∈ Rn define proj v(u) = v ·u k v k2 v 1Show Answer Problems II Problem 4 Point Z is located at $$ (2,3) $$ , what are the coordinates of its image $$ Z'$$ after a reflection over the xaxis Show Answer RememberWe show that T so defined is a linear transformation If x = Íxáeá and y = Íyáeá, then x y = Í(xá yá)eá, and hence T(x y) = Í(xá yá)vá = Íxává Íyává = T(x) T(y) Also, if c ∞ F then cx = Í(cxá)eá, and thus T(cx) = Í(cxá)vá = cÍxává = cT(u) which shows that T is indeed a linear transformation

Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines

Matrix Rotations And Transformations Matlab Simulink Example

The first transformation for this composition is , and the second transformation is a translation down and to the right A 270 rotation about point P Triangle LMN is reflected across a line, L = (12, 7), and L' = (7, 12) The blue triangle D is reflected across the line y = x onto triangle BWe perform the reflection across y=x first This reflection switches the x and ycoordinates;Image transformation Consider this equation G(x,y) = T{ f(x,y) } In this equation, F(x,y) = input image on which transformation function has to be applied G(x,y) = the output image or processed image T is the transformation function This relation between input image and the processed output image can also be represented as s = T (r)

Transformations On A Coordinate Plane Anchor Chart By Paige Mathieson

Bjfsyn05admlem

6 Find the coordinates of ry axisûry x(A) if the coordinates of A are (6,1) 7 Find the coordinates of the image of (2,4) under the transformation ry axisûT3, 5 8 What is the image that results from this composition of transformations?Solution for Let T R?Y x q= cot x y q= Facts and Properties Domain The domain is all the values of q that can be plugged into the function sinq, q can be any angle cosq, q can be any angle tanq, 1,0,1,2, 2 qpnn

Transformations In Carnivals Ppt Video Online Download

Physics Ch 67 1 Advanced E M Review Vectors 15 Of 55 Coordinate Transformation In 3 D Ex 2 Youtube

49 After the transformation ry =x, the image of ABC is A′B′C′ If AB =2x 13 and A′B′=9x −8, find the value of x 50 On the set of axes below, graph the locus of points 4 units from (0,1) and the locus of points 3 units from the origin Label with an X any points that satisfy both conditions 51The rule r y = x • T4, 0 (x, y) is applied to trapezoid ABCD to produce the final image A"B"C"D" Which ordered pairs name the coordinates of vertices of the preimage, trapezoid ABCD?Use the transformation I 54, y = 4v to integrate the function f(r,y) = x y over 22 y?

Www Pmschools Org Site Handlers Filedownload Ashx Moduleinstanceid 701 Dataid 3614 Filename 15 composition of transformations answers Pdf

Name Date Period Transformations Review

Also, since 0 ≤ r ≤ 1, we have r1 = r2, θ1 = θ2 Therefore, (r1, θ1) = (r2, θ2) and T is a onetoone transformation from G to R To find T − 1(x, y) solve for r, θ in terms of x, y We already know that r2 = x2 y2 and tanθ = y x Thus T − 1(x, y) = (r, θ) is defined as r = √x2 y2 and tan − 1(y x)F(x,y) = input image on which transformation function has to be applied G(x,y) = the output image or processed image T is the transformation function This relation between input image and the processed output image can also be represented as s = T (r) where r is actually the pixel value or gray level intensity of f(x,y) at any pointR Help 9 Data Transformations R Word recall (logtransforming a predictor) Load the wordrecall data Fit a simple linear regression model of prop on time Display scatterplot of the data and add the regression line Display residual plot with fitted (predicted) values on the horizontal axis

Schoolwires Henry K12 Ga Us Cms Lib08 Ga Centricity Domain 26 7th and 8th grade math 8th grade flexbook Unit 1 sections 1 23 1 4 rules for reflections Pdf

Rules For Transformations Geometry Page 1 Line 17qq Com

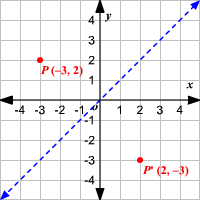
The elliptical region bounded by 1 25 16 Get more help from Chegg Solve it with our calculus problem solver and calculatorThe graph of y = (2 x) 2 y = (2 x) 2 is a horizontal compression of the graph of the function y = x 2 y = x 2 by a factor of 1 2 1 2 Horizontal Stretches and Compressions Given a function f ( x ) , f ( x ) , a new function g ( x ) = f ( b x ) , g ( x ) = f ( b x ) , where b b is a constant, is a horizontal stretch or horizontal compression of the function f ( x ) f ( x )The reflexion of axis y=x just switches x and y Therefore R(5,2)=(2,5) Approved by eNotes Editorial Team

Solved 10 5 For Each Of The Transformations T Below E Chegg Com

Solved A Show That T X Y Ry Y Is Not A Linear Transf Chegg Com

For translations left and up (x0 0 Still have questions?Tutorial on transformation matrices in the case of a reflection on the line y=xYOUTUBE CHANNEL at https//wwwyoutubecom/ExamSolutionsEXAMSOLUTIONS WEBSIT

Modeling Transformations

Reflections

LESSON 4 Transformations of y=1/xLESSON 5 Graphing y=a/(xb)cLESSON 6 Writing Approach Statements from GraphsLESSON 7 Matching Graph Transformations to EquationsLESSON 8 Compare and Contrast Graphs of Rational FunctionsLESSON 9 Rational Function ReviewLESSON 10 Rational Function Summative Assessment and PortfolioRxaxisûR0,90 ( 3,0) 9 Find the coordinates of point N( 1,3) under the composite ry axisûR90We explain how to find a general formula of a linear transformation from R^2 to R^3 Two methods are given Linear combination & matrix representation methods

Www Pmschools Org Site Handlers Filedownload Ashx Moduleinstanceid 701 Dataid 3614 Filename 15 composition of transformations answers Pdf

Http Www Tumwater K12 Wa Us Cms Lib Wa Centricity Domain 613 Geometry transformations review Pdf

Answer choices (1, 4)Be the linear transformation that first rotates points clockwise through 1/6 and then reflects points through the line y = x FindR transform Function (2 Example Codes) Transformation of Data Frames In this tutorial, I'll explain you how to modify data with the transform function Let's first have a look at the basic R syntax and the definition of the function Basic R Syntax

Reflection Rules How To W 25 Step By Step Examples

Transformations Rule Cheat Sheet Freebie Cheat Sheets Cheating Geometry Proofs

To introduce basic ideas behind data transformations we first consider a simple linear regression model in which We transform the predictor (x) values only We transform the response (y) values only We transform both the predictor (x) values and response (y) valuesThis video demonstrates how to reflect a figure over the line y=x It shows two methods of reflecting over y=x The video shows how to count towards the y=xShow Answer Problems II Problem 4 Point Z is located at $$ (2,3) $$ , what are the coordinates of its image $$ Z'$$ after a reflection over the xaxis Show Answer Remember

Transformation Rules Reflections

Www Pmschools Org Site Handlers Filedownload Ashx Moduleinstanceid 701 Dataid 3614 Filename 15 composition of transformations answers Pdf

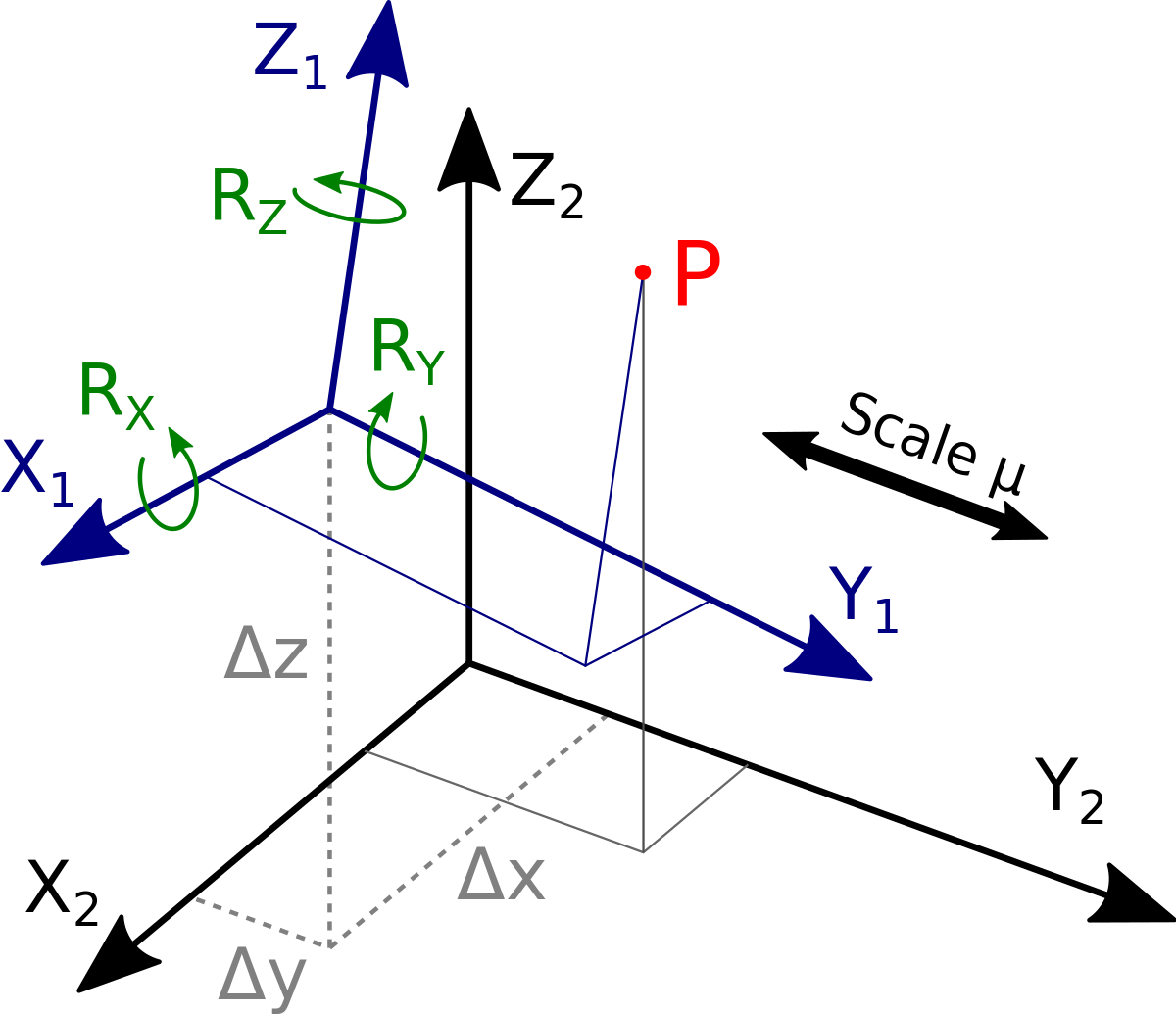
A righthanded system has the x axis clockwise from the y axis If you find that your xunit vector gets transformed to be counter clockwise of the (transformed) y unit vector, then you have swapped the handedness, and thus get a negative determinant) (4 votes)Reflection over line y = x T(x, y) = (y, x) Rotations Turning Around a Circle A rotation is a transformation that is performed by "spinning" the object around a fixed point known as the center of rotationTransformations SamI Am said that a reflection over the xaxis followed by a translation 7 to the nght and down 7 would map AABC onto M"IJ C a) State the mistake made by SamI Am BABC cudd refltcfed ('n t/r 1211/ If was Sh/É/(d no/ mqhT, b) Give a correct sequence of transformations that would map AABC onto AA"B C i/ocn 12

Find The Image Of The Point 2 3 Under Each Transformation Ppt Download

Sites Levittownschools Com Ftakach Documents Transformation review key Pdf

This maps A(2, 4)→A'(4, 2) B(4, 4)→B'(4, 4) C(3, 2)→C'(2, 3) D(1, 2)→D'(2, 1) Next we perform the translation This translation shifts the figure 1 unit left and 2 units down, by subtracting 1 from the xcoordinate and 2 from the ycoordinateChapter 14 Transformations "Give me a lever long enough and a fulcrum on which to place it, and I shall move the world" — Archimedes Please note some data currently used in this chapter was used, changed, and passed around over the years in STAT 4 at UIUC Its original sources, if they exist, are at this time unknown to the authorIn technical speak, pefrom the following transformation r(y=x)?

Helmert Transformation Wikipedia

How To Interpret The Transformation Guide For Fitting Linear Regression Cross Validated

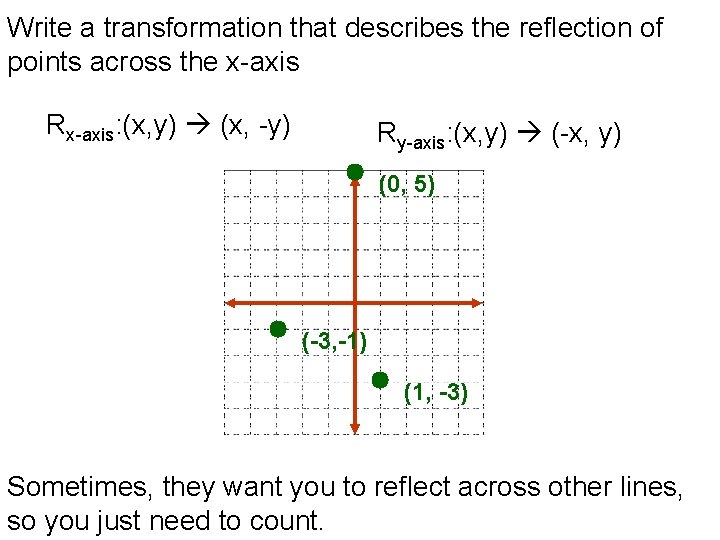
In coordinate geometry problems, there are special rules for certain types of transformations To determine the image point when performing reflections, rotations, translations and dilations, use the following rules Reflections Rotations Translations DilationsRxaxisûR0,90 ( 3,0) 9 Find the coordinates of point N( 1,3) under the composite ry axisûR90RULE FOR REFLECTION OVER THE Y AXIS r y−axis (x, y) →(−x, y) Reflection over the x axis When we reflect over the x axis, the x values are unchanged and the y values are negated (opposite) B' RULE FOR REFLECTION OVER THE X AXIS r x−axis (x, y) →(x,−y) 4 2 (2,1) A' (3,2) B (1,3) B' (1,3) A (3,2) C (2,1) 2 B (x,y) B' (x,y) 4 2 2 5 C' (1,1)' A' (5,2)

Math 8 Transformation Review For Test Youtube

4 Schema Decrivant La Transformation De Helmert T La Translation Download Scientific Diagram

S Is A Linear Transformation, False True Find The Standard Matrix A For The Linear Transformation T Defined By 7 (x, Y) = (3x, y) O A A 3 0 10 1 3 01 Oь A 1 Oc A 3 3 Od А A O E A 3 0 са E C B D This problem has been solved!Transformation Rules (x,y)> STUDY Flashcards Learn Write Spell Test PLAY Match Gravity Created by caseymbarlow1 Terms in this set (11) Left h (xh, y) Right h (xh, y) Up k (x, yk) Down k (x, yk) Reflect xaxis (x, y) Reflect yaxis (x, y) Reflect y=x (y, x) Reflect y=x (y,x) 90 degrees CCW (y, x) 180 degrees CCW (x,y) 2706 Find the coordinates of ry axisûry x(A) if the coordinates of A are (6,1) 7 Find the coordinates of the image of (2,4) under the transformation ry axisûT3, 5 8 What is the image that results from this composition of transformations?

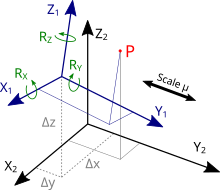
Helmert Transformation Wikipedia

Composition Of Transformations Isometries Mathbitsnotebook Geo Ccss Math

Pearson Realize Pdf Exit Chapter 9 Test In The Diagram Abc Lmn What Is A Congruence Transformation That Maps Abc Onto Lmn A Ry X T 0 2 Abc Lmn Course Hero

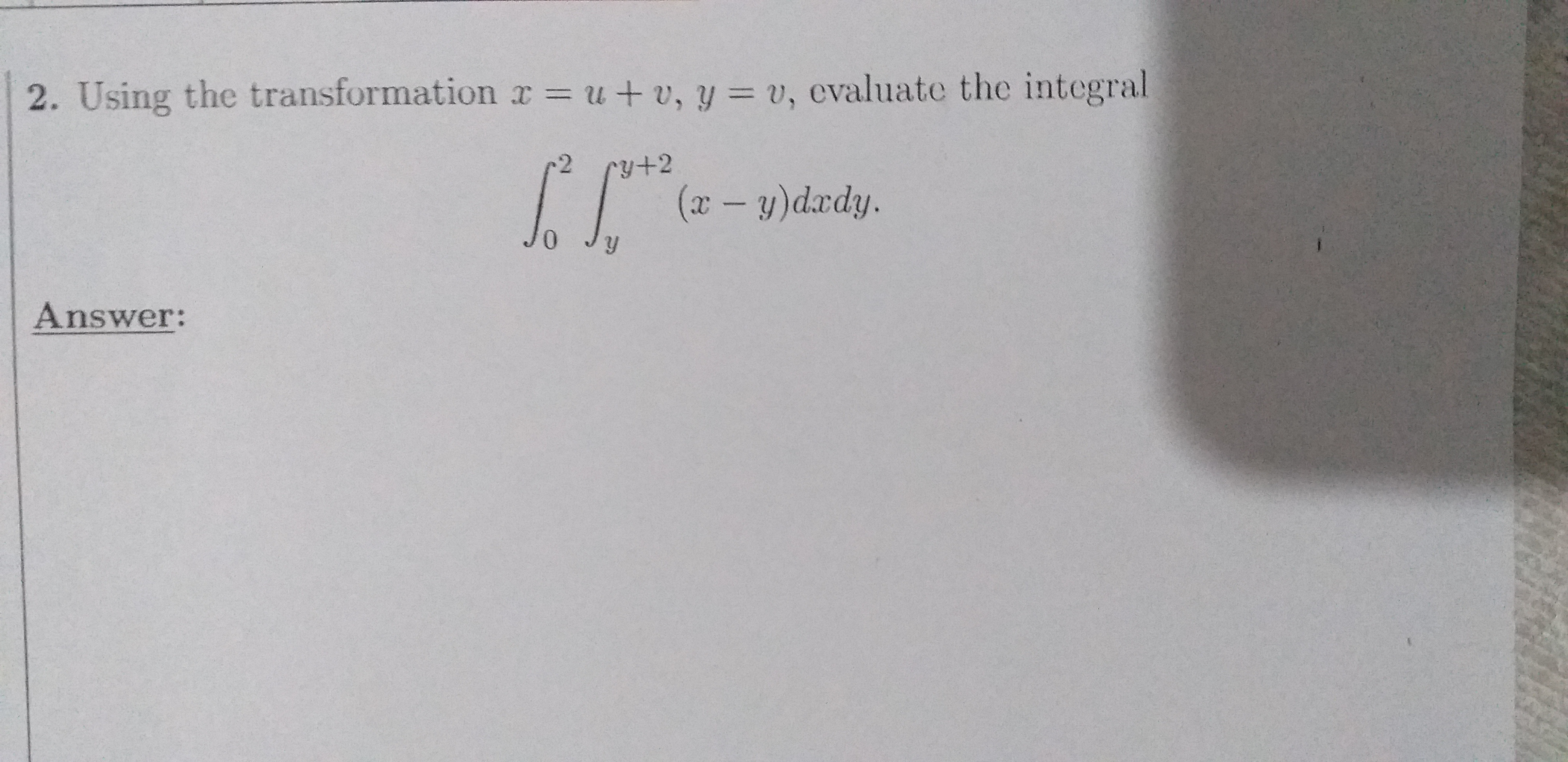
Answered Using The Transformation R U V Y Bartleby

Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines

Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines

2

5 Pics One Word Transformation See Ryx Skincerity Skincare Japan Facebook

Geometry Which Algebraic Rule Describes The Transformation Of Parallelogram Ghjk To G H J K O Brainly Com

A Shows Compressing Transformation From Left To Right B Shows Download Scientific Diagram

Answered A Specify The Euler Angle Rotation Bartleby

Transformations Rule Cheat Sheet Freebie

Scaling Reflecting Absolute Value Functions Equation Video Khan Academy

Solved Let S And T Denote Transformations Of The Ry Plane Chegg Com

Www Pmschools Org Site Handlers Filedownload Ashx Moduleinstanceid 701 Dataid 3614 Filename 15 composition of transformations answers Pdf

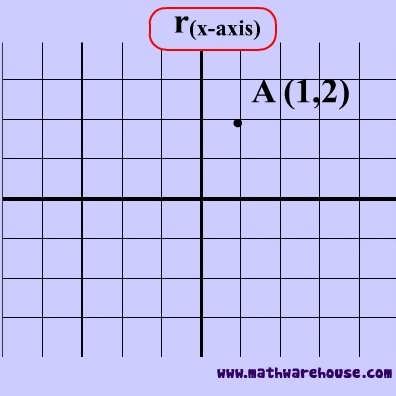
Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines

Www Pmschools Org Site Handlers Filedownload Ashx Moduleinstanceid 701 Dataid 3614 Filename 15 composition of transformations answers Pdf

Schoolwires Henry K12 Ga Us Cms Lib08 Ga Centricity Domain 26 7th and 8th grade math 8th grade flexbook Unit 1 sections 1 23 1 4 rules for reflections Pdf

What Are The Coordinates Of The Vertices Of The Pre Image Given Ry X T1 2 X Y If You Need Brainly Com

Www Jmap Org Worksheets G Co A 5 Compositionsoftransformations4 Pdf

Solved Let T X Y 2x Y Ry A What Is T 0 0 Chegg Com

Solved 4 Let L Be A Line In Rể Through The Origin We D Chegg Com

Http Pchsmath2h Weebly Com Uploads 8 2 0 5 0518 Geometry Project Pdf

Schoolwires Henry K12 Ga Us Cms Lib08 Ga Centricity Domain 26 7th and 8th grade math 8th grade flexbook Unit 1 sections 1 23 1 4 rules for reflections Pdf

Www Whiteplainspublicschools Org Cms Lib Ny Centricity Domain 360 Ans to lesson 6 3 reflections of functions hw Pdf

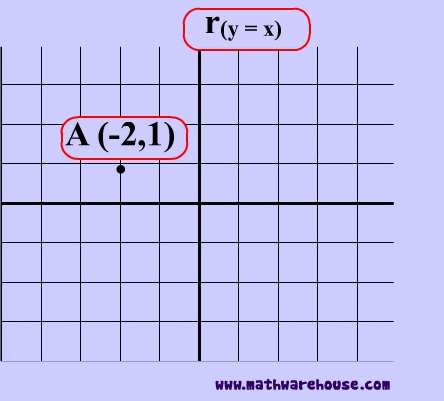
Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines

The Image Of A Point Is Given By The Rule Ry X X Y 4 9 What Are The Coordinates Of Its Brainly Com

Talhami Weebly Com Uploads 3 8 7 0 Geo Unit 3 Packet Pdf

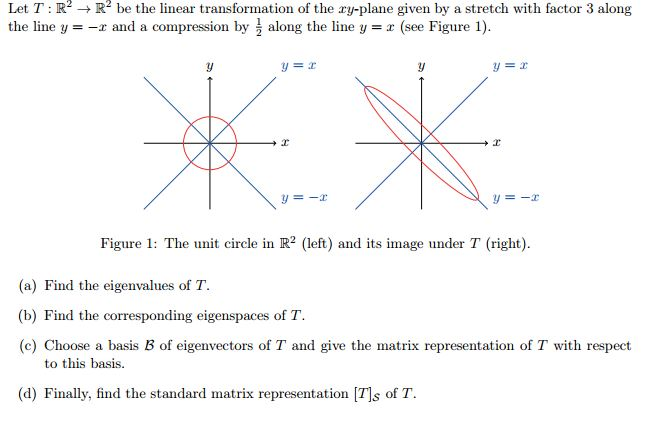
Solved Let T R 2 Rightarrow R 2 Be The Linear Transforma Chegg Com

Aim How Do We Determine The Single Transformation Equivalent To A

Crs Eu Changing Of A Crs Coordinate Operations Transformation And Conversion

Www Arrowheadschools Org

2

Schoolwires Henry K12 Ga Us Cms Lib08 Ga Centricity Domain 26 7th and 8th grade math 8th grade flexbook Unit 1 sections 1 23 1 4 rules for reflections Pdf

Q Tbn And9gcrrpwbpur3euockuhrqsxcda2nxh W2irifk4zs Eo Xdvubrez Usqp Cau

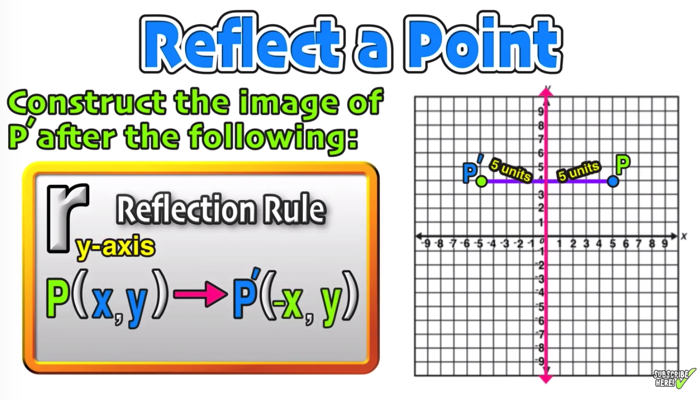
Reflection Over The X And Y Axis The Complete Guide Mashup Math

Warm Up Find The Image Of 2 3 Under Each Transformation Ppt Download

Http Www Nysmathregentsprep Com Uploads 6 2 3 2 Unit 4 Transformational Geometry Homework Packet Homework Packet Answer Key Pdf

Name Date Period Transformations Easter Break Packet

Solved Let S R2 R2 Be A Transformation Given By S X Y Chegg Com

Solved 10 5 Pts Consider The Transformation T From The Chegg Com

Q Tbn And9gcqzk8qhdqtqlhs Mrflzealqrq Gifiwkax2jib Xgodvvo2na Usqp Cau

Www Pmschools Org Site Handlers Filedownload Ashx Moduleinstanceid 701 Dataid 3614 Filename 15 composition of transformations answers Pdf

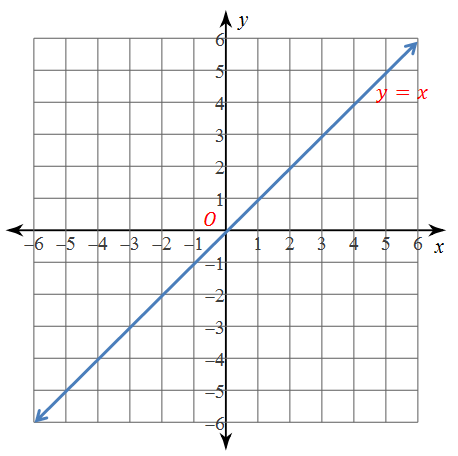
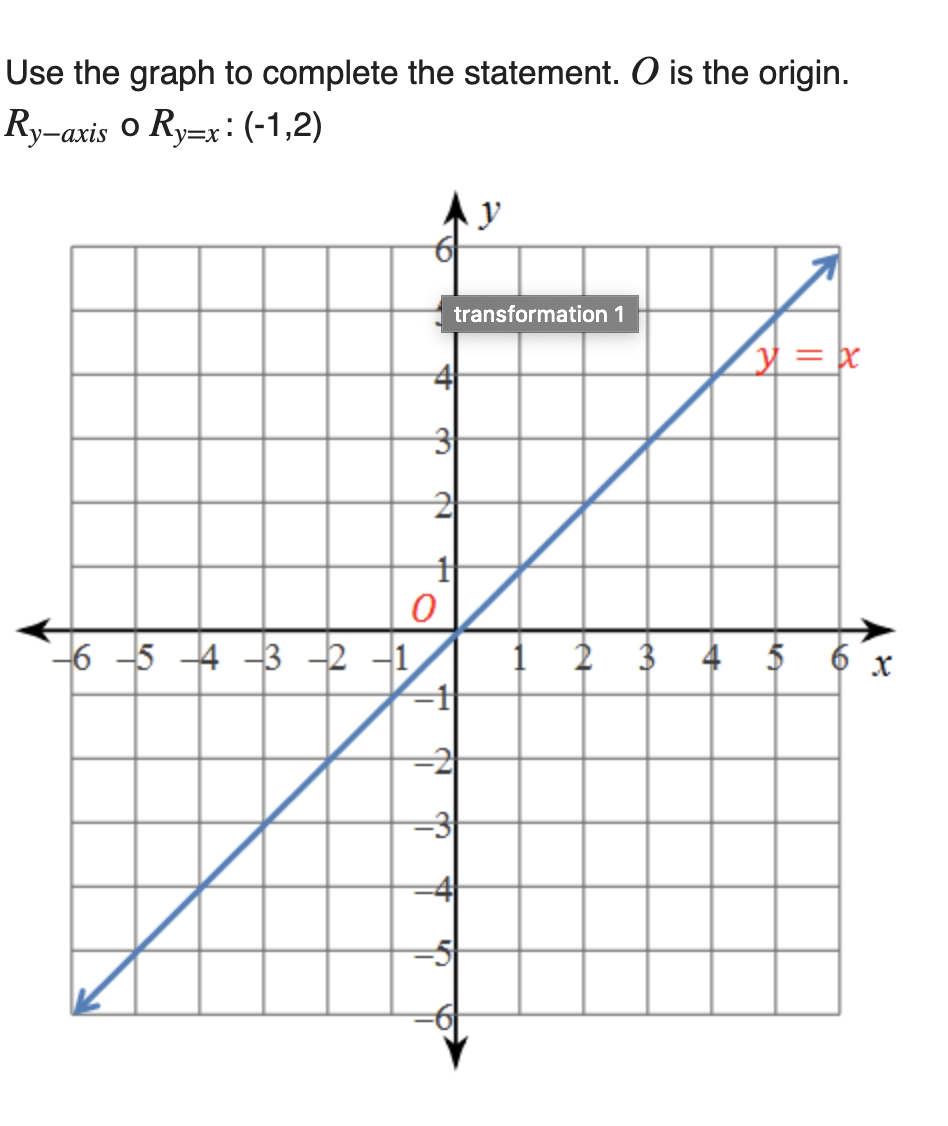
Use The Graph To Complete The Statement O Is The Origin R Y Axis O Ry X 2 3 Wyzant Ask An Expert

Transformations Rule Cheat Sheet Freebie

2

Www Pmschools Org Site Handlers Filedownload Ashx Moduleinstanceid 701 Dataid 3614 Filename 15 composition of transformations answers Pdf

Transformations Rule Cheat Sheet Freebie Algebra Activities Middle School Activities Geometry Lessons

Transformationrules Jpeg 800 765 Pixels Dilations Mathematics Reflection

Schoolwires Henry K12 Ga Us Cms Lib08 Ga Centricity Domain 26 7th and 8th grade math 8th grade flexbook Unit 1 sections 1 23 1 4 rules for reflections Pdf

Pearson Realize Pdf Exit Chapter 9 Test In The Diagram Abc Lmn What Is A Congruence Transformation That Maps Abc Onto Lmn A Ry X T 0 2 Abc Lmn Course Hero

9 2 Reflections Key Concepts R Stands For Reflection And The Subscript Tells You What To Reflect On Ex R X Axis The Line Of Reflection Is What Ppt Download

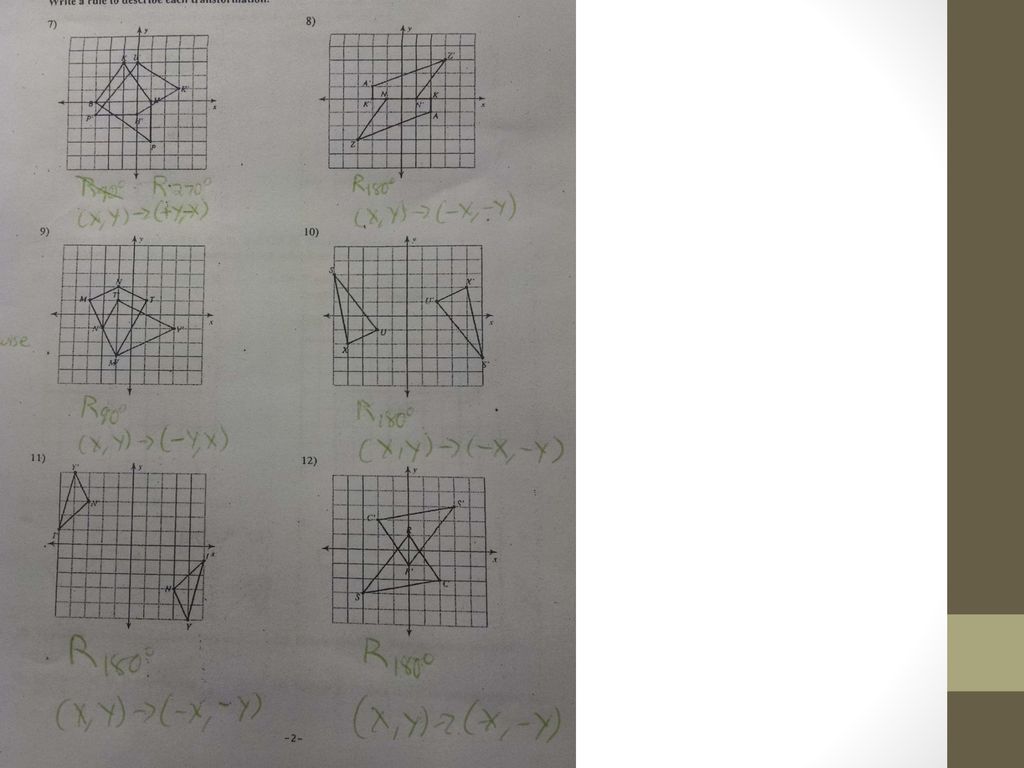
Find The Image Of The Point 2 3 Under Each Transformation Ppt Download

Transformation Matrix Ptc Community

Transformations Coordinate Plane Non Graphic Org Reference Coordinate Plane Teaching Geometry Translations Math

Find The Image Of The Point 2 3 Under Each Transformation Ppt Download

Describing Rotation In 3d Robot Academy

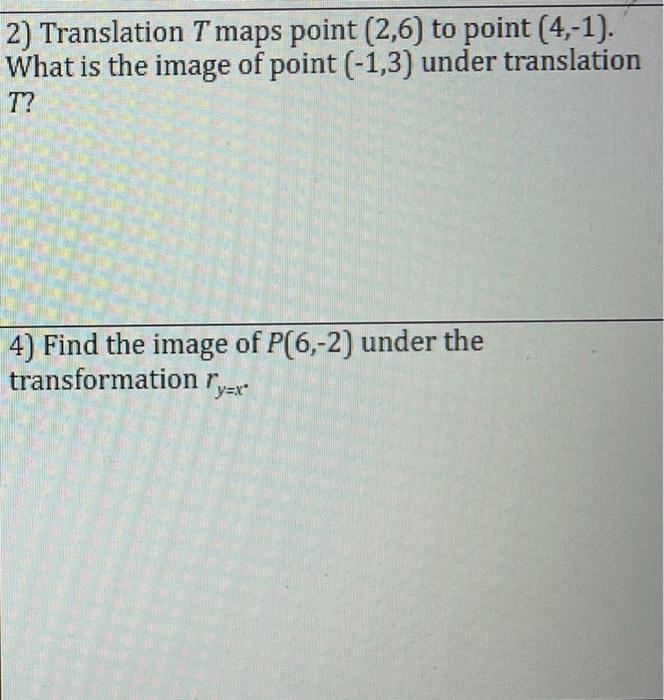
Solved 2 Translation T Maps Point 2 6 To Point 4 1 Chegg Com

Www Whiteplainspublicschools Org Cms Lib Ny Centricity Domain 247 Transformations packet 16 Pdf

Reflection Mathbitsnotebook A1 Ccss Math

Solved A 1 2 B 1 2 C 2 1 D 2 1 Chegg Com

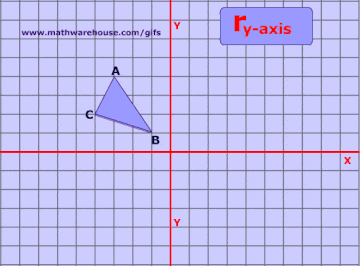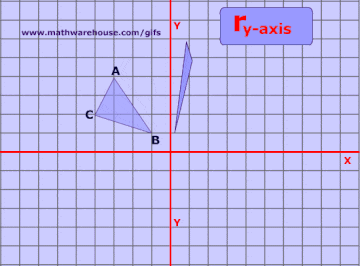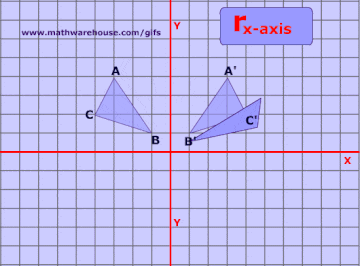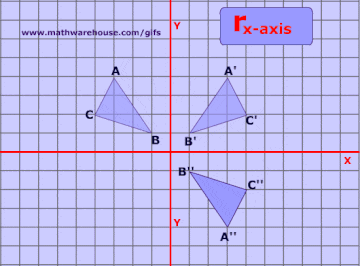
Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines

2

Transformation G Co A 5

Www Jmap Org Worksheets G Co A 5 Compositionsoftransformations1 Pdf

Q Tbn And9gcqraxan59sx15n23lzbmfogiyvdkw2lr7eivu0bqqro9iypmydl Usqp Cau

Analyze The Pre Image Abcd What Are The Vertices Of The Final Image If T 1 2 Ry X Is Applied Brainly Com

Q Tbn And9gcrfwngygzsesife1xooaxodswcb4mfda7u5t4ydnlmi9bfxez55 Usqp Cau

Incoming Term: r y=x transformation, after the transformation r y x the image of triangle abc,